Dalam kehidupan sehari-hari, sering kita jumpai banyak hal yang dapat kita deskripsikan dalam bentuk data. Informasi data yang diperoleh tentunya harus diolah terlebih dahulu menjadi sebuah data yang mudah dibaca dan dianalisa. Statistika adalah ilmu yang mempelajari cara-cara pengolahan data.
Untuk meperoleh data-data tersebut, diperlukan adanya suatu penelitian. Penelitian ini didapatkan melalui berbagai cara, dan juga berbagai langka-langkah pengujian dari para pengumpul data. Sebelum melakukan penelitian, kita akan menduga-duga terlebih dahulu terhadap apa yang kita ingin teliti. Pernyataan dugaan atau pernyataan sementara kita ini yang disebut hipotesis.
A. Pengertian Pengujian Hipotesis
Hipotesis berasal dari bahasa Yunani, Hupo berarti Lemah atau kurang atau di bawah ,Thesis berarti teori, proposisi atau pernyataan yang disajikan sebagai bukti. Sehingga dapat diartikan sebagai Pernyataan yang masih lemah kebenarannya dan perlu dibuktikan atau dugaan yang sifatnya masih sementara.
Hipotesis juga dapat diartikan sebagai pernyataan keadaan populasi yang akan diuji kebenarannya menggunakan data/informasi yang dikumpulkan melalui sampel, dan dapat dirumuskan berdasarkan teori, dugaan, pengalaman pribadi/orang lain, kesan umum, kesimpulan yang masih sangat sementara.
Hipotesis statistik adalah pernyataan atau dugaan mengenai keadaan populasi yang sifatnya masih sementara atau lemah kebenarannya. Hipotesis statistik dapat berbentuk suatu variabel seperti binomial, poisson, dan normal atau nilai dari suatu parameter, seperti rata-rata, varians, simpangan baku, dan proporsi. Hipotesis statistic harus di uji, karena itu harus berbentuk kuantitas untuk dapat di terima atau di tolak. Hipotesis statistic akan di terima jika hasil pengujian membenarkan pernyataannya dan akan di tolak jika terjadi penyangkalan dari pernyataannya.
Pengujian Hipotesis adalah suatu prosedur yang dilakukan dengan tujuan memutuskan apakah menerima atau menolak hipotesis itu. Dalam pengujian hipotesis, keputusan yang di buat mengandung ketidakpastian, artinya keputusan bias benar atau salah, sehingga menimbulkan risiko. Besar kecilnya risiko dinyatakan dalam bentuk probabilitas. Pengujian hipotesis merupakan bagian terpenting dari statistic inferensi (statistic induktif), karena berdasarkan pengujian tersebut, pembuatan keputusan atau pemecahan persoalan sebagai dasar penelitian lebih lanjut dapat terselesaikan.
B. Prosedur Pengujian Hipotesis
Prosedur pengujian hipotesis statistic adalah langkah-langkah yang di pergunakan dalam menyelesaikan pengujian hipotesis tersebut. Berikut ini langkah-langkah pengujian hipotesis statistic adalah sebagai berikut.
1. Menentukan Formulasi Hipotesis
Formulasi atau perumusan hipotesis statistic dapat di bedakan atas dua jenis, yaitu sebagai berikut;
- Hipotesis nol / nihil (HO) : Hipotesis nol adalah hipotesis yang dirumuskan sebagai suatu pernyataan yang akan di uji. Hipotesis nol tidak memiliki perbedaan atau perbedaannya nol dengan hipotesis sebenarnya.
- Hipotesis alternatif/ tandingan (H1 / Ha): Hipotesis alternatif adalah hipotesis yang di rumuskan sebagai lawan atau tandingan dari hipotesis nol. Dalam menyusun hipotesis alternatif, timbul 3 keadaan berikut.
- H1 menyatakan bahwa harga parameter lebih besar dari pada harga yang di hipotesiskan. Pengujian itu disebut pengujian satu sisi atau satu arah, yaitu pengujian sisi atau arah kanan.
- H1 menyatakan bahwa harga parameter lebih kecil dari pada harga yang di hipotesiskan. Pengujian itu disebut pengujian satu sisi atau satu arah, yaitu pengujian sisi atau arah kiri.
- H1 menyatakan bahwa harga parameter tidak sama dengan harga yang di hipotesiskan. Pengujian itu disebut pengujian dua sisi atau dua arah, yaitu pengujian sisi atau arah kanan dan kiri sekaligus.
Secara umum, formulasi hipotesis dapat di tuliskan :
 2. Menentukan Taraf Nyata (α)
2. Menentukan Taraf Nyata (α)
Apabila hipotesis nol (H0) diterima (benar) maka hipotesis alternatif (Ha) di tolak. Demikian pula sebaliknya, jika hipotesis alternatif (Ha) di terima (benar) maka hipotesis nol (H0) ditolak.
Taraf nyata adalah besarnya batas toleransi dalam menerima kesalahan hasil hipotesis terhadap nilai parameter populasinya. Semakin tinggi taraf nyata yang di gunakan, semakin tinggi pula penolakan hipotesis nol atau hipotesis yang di uji, padahal hipotesis nol benar.
Besaran yang sering di gunakan untuk menentukan taraf nyata dinyatakan dalam %, yaitu: 1% (0,01), 5% (0,05), 10% (0,1), sehingga secara umum taraf nyata di tuliskan sebagai α0,01,α0,05, α0,1. Besarnya nilai α bergantung pada keberanian pembuat keputusan yang dalam hal ini berapa besarnya kesalahan (yang menyebabkan resiko) yang akan di tolerir. Besarnya kesalahan tersebut di sebut sebagai daerah kritis pengujian (critical region of a test) atau daerah penolakan ( region of rejection).
Nilai α yang dipakai sebagai taraf nyata di gunakan untuk menentukan nilai distribusi yang di gunakan pada pengujian, misalnya distribusi normal (Z), distribusi t, dan distribusi X². Nilai itu sudah di sediakan dalam bentuk tabel di sebut nilai kritis.
3. Menentukan Kriteria Pengujian
Kriteria Pengujian adalah bentuk pembuatan keputusan dalam menerima atau menolak hipotesis nol (Ho) dengan cara membandingkan nilai α tabel distribusinya (nilai kritis) dengan nilai uji statistiknya, sesuai dengan bentuk pengujiannya. Yang di maksud dengan bentuk pengujian adalah sisi atau arah pengujian.
- Penerimaan Ho terjadi jika nilai uji statistiknya lebih kecil atau lebih besar daripada nilai positif atau negatif dari α tabel. Atau nilai uji statistik berada di luar nilai kritis.
- Penolakan Ho terjadi jika nilai uji statistiknya lebih besar atau lebih kecil daripada nilai positif atau negatif dari α tabel. Atau nilai uji statistik berada di luar nilai kritis.
Dalam bentuk gambar, kriteria pengujian seperti gambar di bawah ini:
 4. Menentukan Nilai Uji Statistik
4. Menentukan Nilai Uji Statistik
Uji statistik merupakan rumus-rumus yang berhubungan dengan distribusi tertentu dalam pengujian hipotesis. Uji statistik merupakan perhitungan untuk menduga parameter data sampel yang di ambil secara random dari sebuah populasi. Misalkan, akan di uji parameter populasi (P), maka yang pertama-tama di hitung adalah statistik sampel (S).
5. Membuat Kesimpulan
Pembuatan kesimpulan merupakan penetapan keputusan dalam hal penerimaan atau penolakan hipotesis nol (Ho)yang sesuai dengan kriteria pengujiaanya. Pembuatan kesimpulan dilakukan setelah membandingkan nilai uji statistik dengan nilai α tabel atau nilai kritis.
- Penerimaan Ho terjadi jika nilai uji statistik berada di luar nilai kritisnya.
- Penolakan Ho terjadi jika nilai uji statistik berada di dalam nilai kritisnya.
Kelima langkah pengujian hipotesis tersebut di atas dapat di ringkas seperti berikut.
Langkah 1 : Menentukan formulasi hipotesis nol (H0) dan hipotesis alternatifnya (Ha)
Langkah 2 : Memilih suatu taraf nyata (α) dan menentukan nilai table.
Langkah 3 : Membuat criteria pengujian berupa penerimaan dan penolakan H0.
Langkah 4 : Melakukan uji statistic
Langkah 5 : Membuat kesimpulannya dalam hal penerimaan dan penolakan H0.
C. Jenis-Jenis Pengujian Hipotesis
Pengujian hipotesis dapat di bedakan atas beberapa jenis berdasarkan criteria yang menyertainya.
1. Berdasarkan Jenis Parameternya
Didasarkan atas jenis parameter yang di gunakan, pengujian hipotesis dapat di bedakan atas tiga jenis, yaitu sebagai berikut .
a. Pengujian hipotesis tentang rata-rata
Pengujian hipotesis tentang rata-rata adalah pengujian hipotesis mengenai rata-rata populasi yang di dasarkan atas informasi sampelnya.
Contohnya:
- Pengujian hipotesis satu rata-rata
- Pengujian hipotesis beda dua rata-rata
- Pengujian hipotesis beda tiga rata-rata
- Pengujian hipotesis tentang proporsi
Pengujian hipotesis tentang proporsi adalah pengujian hipotesis mengenai proporsi populasi yang di dasarkan atas informasi sampelnya.
Contohnya:
- Pengujian hipotesis satu proporsi
- Pengujian hipotesis beda dua proporsi
- Pengujian hipotesis beda tiga proporsi
- Pengujian hipotesis tentang varians
Pengujian hipotesis tentang varians adalah pengujian hipotesis mengenai rata-rata populasi yang di dasarkan atas informasi sampelnya.
Contohnya:
- Pengujian hipotesis tentang satu varians
- Pengujian hipotesis tentang kesamaan dua varians
2. Berdasarkan Jumlah Sampelnya
Didasarkan atas ukuran sampelnya, pengujian hipotesis dapat di bedakan atas dua jenis, yaitu sebagai berikut.
- Pengujian hipotesis sampel besar :Pengujian hipotesis sampel besar adalah pengujian hipotesis yang menggunakan sampel lebih besar dari 30 (n > 30).
- Pengujian hipotesis sampel kecil:Pengujian hipotesis sampel kecil adalah pengujian hipotesis yang menggunakan sampel lebih kecil atau sama dengan 30 (n ≤ 30).
3. Berdasarkan Jenis Distribusinya
Didasarkan atas jenis distribusi yang digunakan, pengujian hipotesis dapat di bedakan atas empat jenis, yaitu sebagai berikut.
a. Pengujian hipotesis dengan distribusi Z
Pengujian hipotesis dengan distribusi Z adalah pengujian hipotesis yang menggunakan distribusi Z sebagai uji statistik. Tabel pengujiannya disebut tabel normal standard. Hasil uji statistik ini kemudian di bandingkan dengan nilai dalam tabel untuk menerima atau menolak hipotesis nol (Ho) yang di kemukakan.
Contohnya :
- Pengujian hipotesis satu dan beda dua rata-rata sampel besar
- Pengujian satu dan beda dua proporsi
- Pengujian hipotesis dengan distribusi t (t-student)
b. Pengujian hipotesis dengan distribusi t
Pengujian hipotesis dengan distribusi t adalah pengujian hipotesis yang menggunakan distribusi t sebagai uji statistik. Tabel pengujiannya disebut tabel t-student. Hasil uji statistik ini kemudian di bandingkan dengan nilai dalam tabel untuk menerima atau menolak hipotesis nol (Ho) yang di kemukakan.
Contohnya :
- Pengujian hipotesis satu rata-rata sampel kecil
- Pengujian hipotesis beda dua rata-rata sampel kecil
- Pengujian hipotesis dengan distribusi χ2 ( chi kuadrat)
c. Pengujian Hipotesi dengan distribusi χ2 ( chi kuadrat)
Pengujian hipotesis dengan distribusi χ2 ( kai kuadrat) adalah pengujian hipotesis yang menggunakan distribusi χ2 sebagai uji statistik. Tabel pengujiannya disebut tabel χ2. Hasil uji statistik ini kemudian di bandingkan dengan nilai dalam tabel untuk menerima atau menolak hipotesis nol (Ho) yang di kemukakan.
Contohnya :
- Pengujian hipotesis beda tiga proporsi
- Pengujian Independensi
- Pengujian hipotesis kompatibilitas
d. Pengujian hipotesis dengan distribusi F (F-ratio)
Pengujian hipotesis dengan distribusi F (F-ratio) adalah pengujian hipotesis yang menggunakan distribusi F (F-ratio) sebagai uji statistik. Tabel pengujiannya disebut tabel F. Hasil uji statistik ini kemudian di bandingkan dengan nilai dalam tabel untuk menerima atau menolak hipotesis nol (Ho) yang di kemukakan.
Contohnya :
- Pengujian hipotesis beda tiga rata-rata
- Pengujian hipotesis kesamaan dua varians
4. Berdasarkan Arah atau Bentuk Formulasi Hipotesisnya
Didasarkan atas arah atau bentuk formulasi hipotesisnya, pengujian hipotesis di bedakan atas 3 jenis, yaitu sebagai berikut.
- Pengujian hipotesis dua pihak (two tail test) : Pengujian hipotesis dua pihak adalah pengujian hipotesis di mana hipotesis nol (Ho) berbunyi “sama dengan” dan hipotesis alternatifnya (H1) berbunyi “tidak sama dengan” (Ho = dan H1 ≠)
- Pengujian hipotesis pihak kiri atau sisi kiri : Pengujian hipotesis pihak kiri adalah pengujian hipotesis di mana hipotesis nol (Ho) berbunyi “sama dengan” atau “lebih besar atau sama dengan” dan hipotesis alternatifnya (H1) berbunyi “lebih kecil” atau “lebih kecil atau sama dengan” (Ho = atau Ho ≥ dan H1 < atau H1≤ ). Kalimat “lebih kecil atau sama dengan” sinonim dengan kata “paling sedikit atau paling kecil”.
- Pengujian hipotesis pihak kanan atau sisi kanan : Pengujian hipotesis pihak kanan adalah pengujian hipotesis di mana hipotesis nol (Ho) berbunyi “sama dengan” atau “lebih kecil atau sama dengan” dan hipotesis alternatifnya (H1) berbunyi “lebih besar” atau “lebih besar atau sama dengan” (Ho = atau Ho ≤ dan H1 > atau H1 ≥). Kalimat “lebih besar atau sama dengan” sinonim dengan kata “paling banyak atau paling besar”.
D. Pengujian Hipotesis Rata-Rata
Pengujian Hipotesis Satu Rata-Rata
1. Sampel besar ( n > 30 )
Untuk pengujian hipotesis satu rata-rata dengan sample besar (n > 30), uji statistiknya menggunakan distribusi Z. Prosedur pengujian hipotesisnya adalah sebagai berikut.
- Formulasi hipotesis
1. Ho : µ = µo
H1 : µ > µo
2. Ho : µ = µo
H1 : µ < µo
3. Ho : µ = µo
H1 : µ ≠ µo
- Penentuan nilai α (taraf nyata) dan nilai Z table (Zα) Menentukan nilai α sesuai soal, kemudian nilai Zα atau Zα/2ditentukan dari tabel.
- Kriteria Pengujian
Untuk Ho : µ = µo dan H1 : µ > µo
o Ho di terima jika Zo ≤ Zα
o Ho di tolak jika Zo > Zα
Untuk Ho : µ = µo dan H1 : µ < µo
o Ho di terima jika Zo ≥ – Zα
o Ho di tolak jika Zo < – Zα
Untuk Ho : µ = µo dan H1 : µ ≠ µo
o Ho di terima jika – Zα/2 ≤ Zo ≤ Zα/2
o Ho di tolak jika Zo > Zα/2 atau Zo < – Zα/2
- Uji Statistik
Simpangan baku populasi ( σ ) di ketahui : 
Simpangan baku populasi ( σ ) tidak di ketahui :
- Kesimpulan
Menyimpulkan tentang penerimaan atau penolakan Ho (sesuai dengan kriteria pengujiannya).
a) Jika H0 diterima maka H1 di tolak
b) Jika H0 di tolak maka H1 di terima
Contoh Soal :
Suatu pabrik susu merek Good Milk melakukan pengecekan terhadap produk mereka, apakah rata-rata berat bersih satu kaleng susu bubuk yang di produksi dan di pasarkan masih tetap 400 gram atau sudah lebih kecil dari itu. Dari data sebelumnya di ketahui bahwa simpangan baku bersih per kaleng sama dengan 125 gram. Dari sample 50 kaleng yang di teliti, di peroleh rata-rata berat bersih 375 gram. Dapatkah di terima bahwa berat bersih rata-rata yang di pasarkan tetap 400 gram? Ujilah dengan taraf nyata 5 % !
Penyelesaian :
Diketahui :
n = 50, X = 375, σ = 125, µo = 400
Jawab :
Formulasi hipotesisnya :
Ho : µ = 400
H1 : µ < 400
Taraf nyata dan nilai tabelnya :
α = 5% = 0,05
Z0,05 = -1,64 (pengujian sisi kiri)
Kriteria pengujian :
o Ho di terima jika Zo ≥ – 1,64
o Ho di tolak jika Zo < – 1,64
Uji Statistik
Kesimpulan
Karena Zo = -1,41 ≥ – Z0,05 = – 1,64 maka Ho di terima. Jadi, berat bersih rata-rata susu bubuk merek GOOD MILK per kaleng yang di pasarkan sama dengan 400 gram
2. Sampel Kecil (n ≤ 30)
Untuk pengujian hipotesis satu rata-rata dengan sampel kecil (n ≤ 30), uji statistiknya menggunakan distribusi t. Prosedur pengujian hipotesisnya adalah sebagai berikut.
- Formulasi hipotesis
1. Ho : µ = µo
H1 : µ > µo
2. Ho : µ = µo
H1 : µ < µo
3. Ho : µ = µo
H1 : µ ≠ µo
- Penentuan nilai α (taraf nyata) dan nilai t- tabel : Menentukan nilai α sesuai soal, kemudian menentukan derajat bebas, yaitu db = n – 1, lalu menentukan nilai tα;n-1 atau tα/2;n-1ditentukan dari tabel.
- Kriteria Pengujian
Untuk Ho : µ = µo dan H1 : µ > µo
o Ho di terima jika to ≤ tα
o Ho di tolak jika to > tα
Untuk Ho : µ = µo dan H1 : µ < µo
o Ho di terima jika to ≥ – tα
o Ho di tolak jika to < – tα
Untuk Ho : µ = µo dan H1 : µ ≠ µo
o Ho di terima jika – tα/2 ≤ to ≤ tα/2
o Ho di tolak jika to > tα/2 atau to < – tα/2
- Uji Statistik
Simpangan baku populasi ( σ ) di ketahui :
Simpangan baku populasi ( σ ) tidak di ketahui :
- Menyimpulkan tentang penerimaan atau penolakan Ho(sesuai dengan criteria pengujiannya).Kesimpulan
a) Jika H0 diterima maka H1 di tolak
b) Jika H0 di tolak maka H1 di terima
Contoh soal :
Sebuah sample terdiri atas 15 kaleng susu, memiliki isi berat kotor seperti yang di berikan berikut ini.
( Isi berat kotor dalam kg/kaleng)
1,21 1,21 1,23 1,20 1,21
1,24 1,22 1,24 1,21 1,19
1,19 1,18 1,19 1,23 1,18
Jika di gunakan taraf nyata 1%, dapatkah kita menyakini bahwa populasi cat dalam kaleng rata-rata memiliki berat kotor 1,2 kg/kaleng ? (dengan alternatif tidak sama dengan). Berikan evaluasi anda !
Penyelesaian :
Diketahui :
n = 15, α= 1%, µo = 1,2
Jawab:
∑X = 18,13
∑X2 = 21,9189
X = 18,13 / 15
= 1,208
Formulasi hipotesisnya :
Ho : µ = 1,2
H1 : µ ≠ 1,2
Taraf nyata dan nilai tabelnya :
α = 1% = 0,01
tα/2 = 0,005 dengan db = 15-1 = 14
t0,005;14 = 2,977
Kriteria pengujian :
o Ho di terima apabila : – 2,977 ≤ to ≤ – 2,977
o Ho di tolak : to > 2,977 atau to < – 2,977
Uji Statistik
Kesimpulan
Karena –t0,005;14 = -2,977 ≤ to = 1,52 ≤ t0,005;14 = – 2,977 maka Hodi terima. Jadi, populasi susu dalam kaleng secara rata-rata berisi berat kotor 1,2 kg/kaleng.
Pengujian Hipotesis Beda Dua Rata-Rata
1. Sampel besar ( n > 30 )
Untuk pengujian hipotesis beda dua rata-rata dengan sampel besar (n > 30), uji statistiknya menggunakan distribusi Z.
Contoh Soal :
Seseorang berpendapat bahwa rata-rata jam kerja buruh di daerah A dan B sama dengan alternatif A lebih besar dari pada B. Untuk itu, di ambil sample di kedua daerah, masing-masing 100 dan 70 dengan rata-rata dan simpangan baku 38 dan 9 jam per minggu serta 35 dan 7 jam per minggu. Ujilah pendapat tersebut dengan taraf nyata 5% ! Untuk Varians/ simpangan baku kedua populasi sama besar !
Penyelesaian :
Diketahui :
n1 = 100 X1 = 38 s₁ = 9
n2 = 70 X2 = 35 s₂ = 7
Jawab:
Formulasi hipotesisnya :
Ho : µ₁ = µ₂
H1 : µ₁ > µ₂
Taraf nyata dan nilai tabelnya :
α = 5% = 0,05
Z0,05 = 1,64 (pengujian sisi kanan)
Kriteria pengujian :
o Ho di terima jika Zo ≤ 1,64
o Ho di tolak jika Zo > 1,64
Uji Statistik
Kesimpulan
Karena Zo = 2,44 > Z0,05 = 1,64 maka Ho di tolak. Jadi, rata-rata jam kerja buruh di daerah A dan daerah B adalah tidak sama.
2. Sampel kecil ( n ≤ 30 )
Untuk pengujian hipotesis beda dua rata-rata dengan sampel kecil (n ≤ 30), uji statistiknya menggunakan distribusi t.
Contoh Soal :
Sebuah perusahan mengadakan pelatihan teknik pemasaran. Sampel sebanyak 12 orang dengan metode biasa dan 10 orang dengan terprogram. Pada akhir pelatihan di berikan evaluasi dengan materi yang sama. Kelas pertama mencapai nilai rata-rata 75 dengan simpangan baku 4,5. Ujilah hipotesis kedua metode pelatihan, dengan alternative keduanya tidak sama! Gunakan taraf nyata 10%! Asumsikan kedua populasi menghampiri distribusi normal dengan varians yang sama!
Penyelesaian :
Diketahui :
n1 = 12 X1 = 80 s₁ = 4
n2 = 10 X2 = 75 s₂ = 4,5
Jawab:
Formulasi hipotesisnya :
Ho : µ₁ = µ₂
H1 : µ₁ ≠ µ₂
Taraf nyata dan nilai tabelnya :
α = 10% = 0,10
db = 12 + 10 – 2 = 20
t0,05;20 = 1,725
Kriteria pengujian :
o Ho di terima apabila -1,725 ≤ t0 ≤ 1,725
o Ho di tolak apabila t0 > 1,725 atau t0 < -1,725
Uji Statistik
Kesimpulan
Karena t0 = 2,76 > t0,05;20 = 1,725 maka Ho di tolak. Jadi, kedua metode yang digunakan dalam pelatihan tidak sama hasilnya.
Kesimpulan
Hipotesis berasal dari bahasa Yunani, Hupo berarti Lemah atau kurang atau di bawah ,Thesis berarti teori, proposisi atau pernyataan yang disajikan sebagai bukti. Sehingga dapat diartikan sebagai Pernyataan yang masih lemah kebenarannya dan perlu dibuktikan atau dugaan yang sifatnya masih sementara.
Pengujian Hipotesis adalah suatu prosedur yang dilakukan dengan tujuan memutuskan apakah menerima atau menolak hipotesis itu. Dalam pengujian hipotesis, keputusan yang di buat mengandung ketidakpastian, artinya keputusan bias benar atau salah, sehingga menimbulkan risiko.
- Prosedur Pengujian hipotesis
Ø Langkah 1 : Menentukan formulasi hipotesis nol (H0) dan hipotesis alternatifnya (Ha).
Ø Langkah 2 : Memilih suatu taraf nyata (α) dan menentukan nilai table.
Ø Langkah 3 : Membuat criteria pengujian berupa penerimaan dan penolakan H0.
Ø Langkah 4 : Melakukan uji statistik
Ø Langkah 5 : Membuat kesimpulannya dalam hal penerimaan dan penolakan H0.
- Jenis-Jenis Pengujian Hipotesis
Berdasarkan Jenis Parameternya
- Pengujian hipotesis tentang rata-rata
- Pengujian hipotesis tentang proporsi
- Pengujian hipotesis tentang varians
Berdasarkan Jumlah Sampelnya
- Pengujian hipotesis sampel besar (n > 30).
- Pengujian hipotesis sampel kecil (n ≤ 30).
Berdasarkan Jenis Distribusinya
- Pengujian hipotesis dengan distribusi Z
- Pengujian hipotesis dengan distribusi t (t-student)
- Pengujian hipotesis dengan distribusi χ2 ( kai kuadrat)
- Pengujian hipotesis dengan distribusi F (F-ratio)
Berdasarkan Arah atau Bentuk Formulasi Hipotesisnya
- Pengujian hipotesis dua pihak (two tail test)
- Pengujian hipotesis pihak kiri atau sisi kiri
- Pengujian hipotesis pihak kanan atau sisi kanan
LINK DOWLOAD
Daftar Pustaka
Iqbal, M Hasan. 2002. Pokok-pokok materi statistik 2 (statistik intensif). Jakarta : Bumi Aksara
http://iftitahprimasanti.blogspot.co.id/2012/05/uji-hipotesis.html










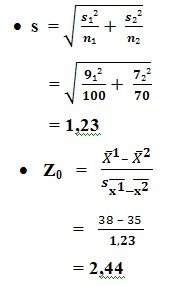



7 Comments
Thanks for education… wish Allah bless u
terimakasih pak
Itu 2.76 bisa di perjelas gimana ngitungnya?
Buatlah data hipotesis minimal sebanyak 30 unit data. Untuk persamaan regresi berganda dengan dua variabel bebas. Mofel regresi berganda dengan dua variabel.
Y= a+β1×1+β2×2+€
Y= produksi padi sawah (kg)
X1= luas lahan (are)
X2= jumlah tenaga kerja (HKP)
Duga besaran
a,β1,β2
Rumuskan dan uji hipotesis pengujian model (uji f)
Interpretasi hasilnya
Assalamualaikum wr.wb
Pak bisa bantuin aku ajarin tugas uji statistik uji dua pihak menggunakan tabel T?
Semua penjelasannya sangat jelas sekali , dan para pembaca juga mudah memahaminya, saya sangat bersyukur sekali bisa menemukan penjelasan seperti ini, karena dengan penjelasan semua yang berada disini memudahkan saya dalam memahami banyak hal. Terutama di bagian penjelasan hipotesis nya sangat menarik minat saya untuk terus membaca.
Keren Pak!!! Lengkap dan mudah dimengerti.